Quick Sort Algorithm

This blog post explains the Quick Sort Algorithm and its implementation using the C programming language. So before writing the C code for the Quick Sort let’s first understand the QuickSort algorithm.

What is Quick Sort Algorithm:

Quick Sort is one of the most popular sorting algorithms. Like the Merge Sort, QuickSort is also based on the divide and conquer strategy. Now you are thinking about what is divide and conquer strategy.

“The divide and conquer is an algorithm design technique. It recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem”.

QuickSort works by selecting a ‘pivot‘ element from the array and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the ‘pivot‘. For this reason, QuickSort is also called partition exchange sort.

There are many different ways to choose the ‘pivot‘,

Choose the first element as ‘pivot‘ .
Choose the last element as ‘pivot‘.
We can choose random element as ‘pivot‘.
We can choose median as ‘pivot‘.

Note: However, always choosing the last element in the partition as the pivot in this way results in poor performance ( $O(n²)$ ) on already sorted arrays or arrays of identical elements.

QuickSort Algorithm Steps:

Let’s see the required steps to sort a list using the QuickSort algorithm.

1. Choose the Pivot Element:

In the beginning, we have already discussed the ways to select the pivot elements. Here, we are selecting the last element of the array as the pivot element.

3 ,7 ,8 ,5 ,2 , 1, 9 ,5, `4`

2. Reorder (Partition) all the array elements around the pivot:

Let’s see a pseudo code to understand this concept. The below method is adopted from the CLRS book.

/* partition function takes last element as pivot and places
   the pivot element at its correct position. It means all
   smaller element will be plaved to left all greater elements
   to right of pivot
 */
int partition(arr[],  start,  end)
{
    // pick last element as pivot
    pivot = arr[end];

    i = (start - 1)  // Index of smaller element and indicates the
        // right position of pivot found so far

    for (j = start; j <= (end- 1); ++j)
    {
        // If current element is smaller than the pivot
        if (arr[j] < pivot)
        {
            i++;    // increment index of smaller element
            swap arr[i] and arr[j]
        }
    }
    swap arr[i + 1] and arr[end]
    return (i + 1);
}

Explanation of the above `pseudo code:`

arr[] = {3, 7, 8, 5, 2, 1, 9, 5, 4}
Indexes: 0  1  2  3  4  5  6  7  8


start = 0, end =  8, pivot = arr[h] = 4
Initialize index of smaller element, i = -1





Traverse elements from j = start to end-1
j = 0 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 0 
arr[] = {3, 7, 8, 5, 2, 1, 9, 5, 4}// No change as i and j 
                                     // are same both are 0


j = 1 : Since arr[j] > pivot, do nothing
// No change in i and arr[]


j = 2 : Since arr[j] > pivot, do nothing
// No change in i and arr[]


j = 3 : Since arr[j] > pivot, do nothing
// No change in i and arr[]



j = 4 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 1
arr[] = {3, 2, 8, 5, 7, 1, 9, 5, 4} // We swap 2 and 7 


j = 5 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 2
arr[] = {3, 2, 1, 5, 7, 8, 9, 5, 4} // We swap 1 and 8 


j = 6 : Since arr[j] > pivot, do nothing
// No change in i and arr[]


j = 7 : Since arr[j] > pivot, do nothing
// No change in i and arr[]



We come out of loop because j is now equal to end-1.
Finally we place pivot at correct position by swapping
arr[i+1] and arr[end] (or pivot) 

arr[] = {3, 2, 1, 4, 7, 8, 9, 5, 5} // We swap 4 and 5 


Now 4 is at its correct place. All elements smaller than
4 are before it and all elements greater than 4 are after
it.

3. Apply the above steps recursively to both sub-lists on the left and right of the pivot

Let’s seen an image for better understanding, it explains all the steps taken by the quick Sort to sort the given random set of elements. It is an expanded version of the above steps and also chosen the last element is as ‘pivot‘. You can see the below image in which the shaded element is the pivot.

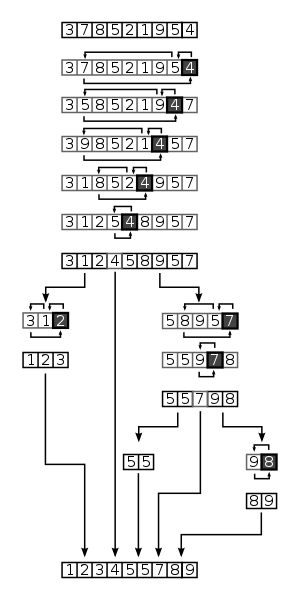
Now let’s see the example code for the QuickSort Algorithm using the C programming language.

#include <stdio.h>

//function to swap variable
void swap(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

/* partition function takes last element as pivot and places
   the pivot element at its correct position. It means all
   smaller element will be placed to left all greater elements
   to right of pivot
 */
int partition (int arr[], int start, int end)
{
    int pivot = arr[end]; // pivot
    int i = (start - 1);
    int j = start;

    for (j = start; j <= (end - 1); j++)
    {
        // If current element is smaller than the pivot
        if (arr[j] < pivot)
        {
            i++; // increment index of smaller element
            swap(&arr[i], &arr[j]);
        }
    }
    swap(&arr[i + 1], &arr[end]);

    return (i + 1);
}

/*
arr[] --> Array to be sorted,
start --> Starting index,
end --> Ending index */
void quickSort(int arr[], int start, int end)
{
    if (start < end)
    {
        // find the pivot element such that
        // elements smaller than pivot are on left of pivot
        // elements greater than pivot are on right of pivot
        int pi = partition(arr, start, end);

        // recursive call on the left of pivot
        quickSort(arr, start, pi - 1);

        // recursive call on the right of pivot
        quickSort(arr, pi + 1, end);
    }
}

//print array element
void printArray(int arr[], int size)
{
    int i;
    for (i = 0; i < size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}


int main()
{
    int arr[] = {3, 7, 8, 5, 2, 1, 9, 5, 4};
    int arr_size = sizeof(arr) / sizeof(arr[0]);

    quickSort(arr, 0, arr_size - 1);

    printf("Sorted array: \n");

    printArray(arr, arr_size);

    return 0;
}

Output: 1 2 3 4 5 5 7 8 9

Quicksort Complexity

Time Complexity
Best	O(n*log n)
Worst	O(n²)
Average	O(n*log n)
Space Complexity	O(log n)
Stability	No