This blog post explains the merge sort algorithm and its implementation using the C programming language. So before writing the C code for the merge sort let’s first understand the merge sort algorithm.

What is Merge Sort Algorithm:

Merge Sort is one of the most popular sorting algorithms and it is an example of the divide and conquer strategy. Now you are thinking about what is divide and conquer strategy.

The divide and conquer is an algorithm design technique. This algorithm recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem.

Consider the below image to better understand how we can sort the given array (38, 27, 43, 3, 9, 82, 10) in increasing order using the divide and conquer algorithm. (Upper half splitting into sublists and the lower half merging the sorted sublists into the one sorted sublist).

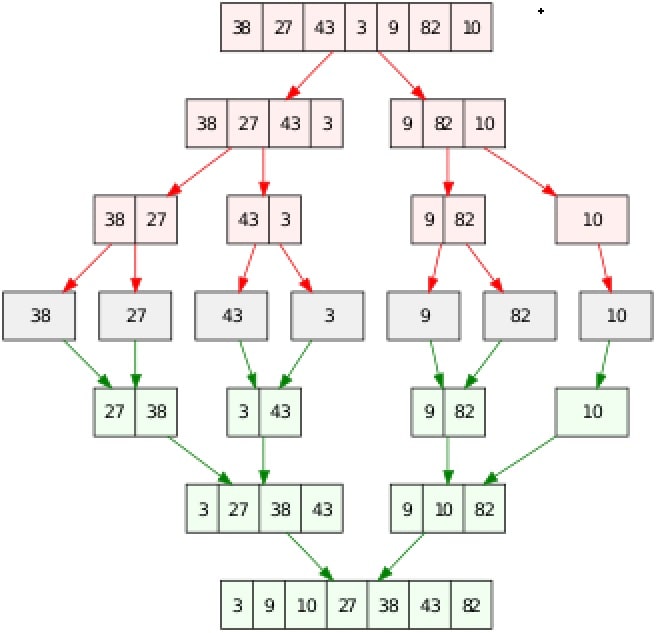
For Now, I am not going to deep dive into the divide and conquer algorithm.  We will cover it in a separate article. So let’s come on to our original topic  “Merge Sort”.

Merge Sort Algorithm:

The mergeSort function repeatedly divides the input array into two halves (subarrays) until we reach a stage where the halve (subarray) contains one element( subarray of size 1).

After that, the merge function comes into pictures and it repeatedly merges the subarray to produce a new sorted subarray until there is only one sorted subarray remaining.

void mergeSort(int arr[], int left, int right)
{
    if (left < right)
    {
        //Middle point to divide the array into two halves
        int m = (right + left) / 2;

        // Sort first and second halves
        mergeSort(arr, left, m);
        mergeSort(arr, m + 1, right);

        //merge sorted sublists
        merge(arr, left, m, right);
    }
}

Note: An array of one element is considered sorted.

Code for Merge Sort Algorithm

You must know recursion to understand this example code. So it is my advice if you are not familiar with recursion, you should read it. Now let’s understand that how we will merge the two subarrays arr[left..median] and arr[median+1..right] to create a sorted array arr[left..right].

We are using the below steps in the merge function:

1. Create copies of the subarrays L ← arr[left..median] and R← arr[median+1..right].

int i, j, k;
int n1 = median - left + 1;
int n2 = right - median;

// create temp arrays
int L[n1], R[n2];

// Copy data to temp arrays L[] and R[]
for (i = 0; i < n1; i++)
{
    L[i] = arr[left + i];
}
for (j = 0; j < n2; j++)
{
    R[j] = arr[median + 1 + j];
}

2. Create three variables i, j, and k.

• ‘i’ maintain the current index of L, starting at the 0th index.
• ‘j’ maintains the current index of R, starting at the 0th index.
• ‘k’ maintains the current index of arr[left..right], starting at left .

i = 0; // Initial index of first subarray

j = 0; // Initial index of second subarray

k = left; // Initial index of merged subarray

3. Until we reach the end of either L or R, pick the smaller among the elements from L and R and place them in the correct position at arr[left..right].

while (i < n1 && j < n2) //check end of L or R
{
    if (L[i] <= R[j])
    {
        arr[k] = L[i];
        i++; //increment index of subarray L
    }
    else
    {
        arr[k] = R[j];
        j++; //increment index of subarray R
    }
    k++; //Increment index of merged array
}

4. When we run out of elements in either L or R, pick up the remaining elements and put them in arr[left..right].

/* Copy the remaining elements of L[], if there
are any */
while (i < n1)
{
    arr[k] = L[i];
    i++;
    k++;
}

/* Copy the remaining elements of R[], if there
are any */
while (j < n2)
{
    arr[k] = R[j];
    j++;
    k++;
}

Now let’s see the example code for the Merge Sort Algorithm using the C programming language.

#include <stdio.h>
#include <stdlib.h>

// Merges two subarrays of arr[].
// First subarray is arr[left..median]
// Second subarray is arr[median+left..right]
void merge(int arr[], int left, int median, int right)
{
    int i, j, k;
    int n1 = median - left + 1;
    int n2 = right - median;

    // create temp arrays
    int L[n1], R[n2];

    // Copy data to temp arrays L[] and R[]
    for (i = 0; i < n1; i++)
    {
        L[i] = arr[left + i];
    }
    for (j = 0; j < n2; j++)
    {
        R[j] = arr[median + 1 + j];
    }

    // Merge the temp arrays back into arr[left..right]
    i = 0; // Initial index of first subarray
    j = 0; // Initial index of second subarray
    k = left; // Initial index of merged subarray
    while (i < n1 && j < n2)
    {
        if (L[i] <= R[j])
        {
            arr[k] = L[i];
            i++;
        }
        else
        {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    /* Copy the remaining elements of L[], if there
    are any */
    while (i < n1)
    {
        arr[k] = L[i];
        i++;
        k++;
    }

    /* Copy the remaining elements of R[], if there
    are any */
    while (j < n2)
    {
        arr[k] = R[j];
        j++;
        k++;
    }
}

/* left is for left index and right is right index of the
sub-array of arr to be sorted */
void mergeSort(int arr[], int left, int right)
{
    if (left < right)
    {
        //Middle point to divide the array into two halves
        int m = (right + left) / 2;

        // Sort first and second halves
        mergeSort(arr, left, m);
        mergeSort(arr, m + 1, right);

        //merge sorted sublists
        merge(arr, left, m, right);
    }
}

//print array element
void printArray(int arr[], int size)
{
    int i;
    for (i = 0; i < size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}


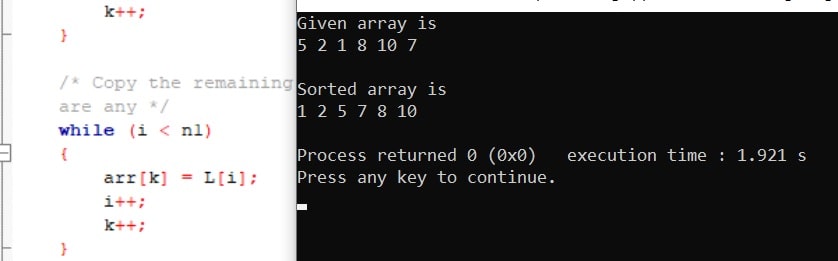
int main()
{
    int arr[] = {5, 2, 1, 8, 10, 7 };
    int arr_size = sizeof(arr) / sizeof(arr[0]);

    printf("Given array is \n");
    printArray(arr, arr_size);

    mergeSort(arr, 0, arr_size - 1);

    printf("\nSorted array is \n");
    printArray(arr, arr_size);

    return 0;
}

Output:

Analysis:

The input array is divided into two parts recursively in the merge sort. If I assume T(n) is the complexity of Merge sort with n elements. So time complexity of the Merge Sort can be expressed as following recurrence relation. T(n) = 2T(n/2) + θ(n). But using the Master Theorem we can get T(n) = θ(nLogn).

Time Complexity:

• Best Case Complexity: O(n*log n)
• Worst Case Complexity: O(n*log n)
• Average Case Complexity: O(n*log n)

Space Complexity:

• The space complexity of merge sort is O(n).

Recommended Articles for you:

• Insertion Sort Algorithm.
• Quick Sort Algorithm.
• Selection Sort Algorithm.
• Bubble Sort Algorithm in C.
• Radix Sort Algorithm.
• Counting Sort Algorithm.
• Why is it faster to process sorted array than an unsorted array?
• How to access 2d array in C?
• Array interview questions.
• How to create dynamic array in C?
• How to pass an array as a parameter in C?