This blog post explains, “how to find inversion count or the number of inversions” in a given array using the merge sort algorithm. I will also implement an example code using the C programming language to explain the inversions counting. The prerequisite of this post is that you should have basic knowledge of the merge sort algorithm.
If you don’t have the knowledge of the merge sort algorithm you can check this blog post “Understanding of the merge sort algorithm”. Also before explaining the problem and its solution, let’s first understand the meaning of inversions in the array.
What is the meaning of inversions in an array?
The number of inversions in an array means that the number of changes required in the array for it to be sorted. We can also categorize the sorting algorithm on the basis of inversions count (by the number of swaps).
So here we see how many swaps are required to sort an array using the merge sort. If the given array is already sorted, the inversion count will be 0. But it will be maximum when the array is reversely sorted(descending order). This question asks by many reputed product-based companies in their technical interview. Now time to understand the problem.
Understanding the Problem:
Given an integers array arr[], if i < j and arr[i] > arr[j] then the elements at indices i and j form an inversion, and the pair (i, j) is called the inversion of an array. You need to write a program to find the total counts of inversion in an array arr[].
Example,
Input1: int arr[] = {3, 2, 1}
Output1: 3
Explanation:
Inversion pairs in the given array are
(3,2), (3,1) and (2,1). Thus, the count of inversion is 3.
Input2: int arr[] = {2, 1}
Output2: 1
Explanation:
Inversion pairs in the given array is (2,1).
Input3: int arr[] = {1, 1, 1, 2, 2}
Output3: 0
Explanation:
Given array is already sorted, so there are no inversions.
Solution of the problem using the Merge Sort:
We know that merge sort based on the Divide and Conquer algorithm. So this solution will be also based on the divide and conquer algorithm. This algorithm recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly.
So here we will divide our given input array into two halves. For each half, we will be getting the inversion counts using recursion. Suppose the number of inversions in the left half and right half of the array is cnt1 and cnt2. Because during the merge process, the inversion count (cross inversion) is found by comparing elements of both halves. So suppose the inversion count during merging is cnt3.
The total counts of inversion will be the sum of inversions in the first half, the second half as well as the inversion counts during the process of merging.
Total Inversion Count = cnt1 + cnt2 + cnt3;
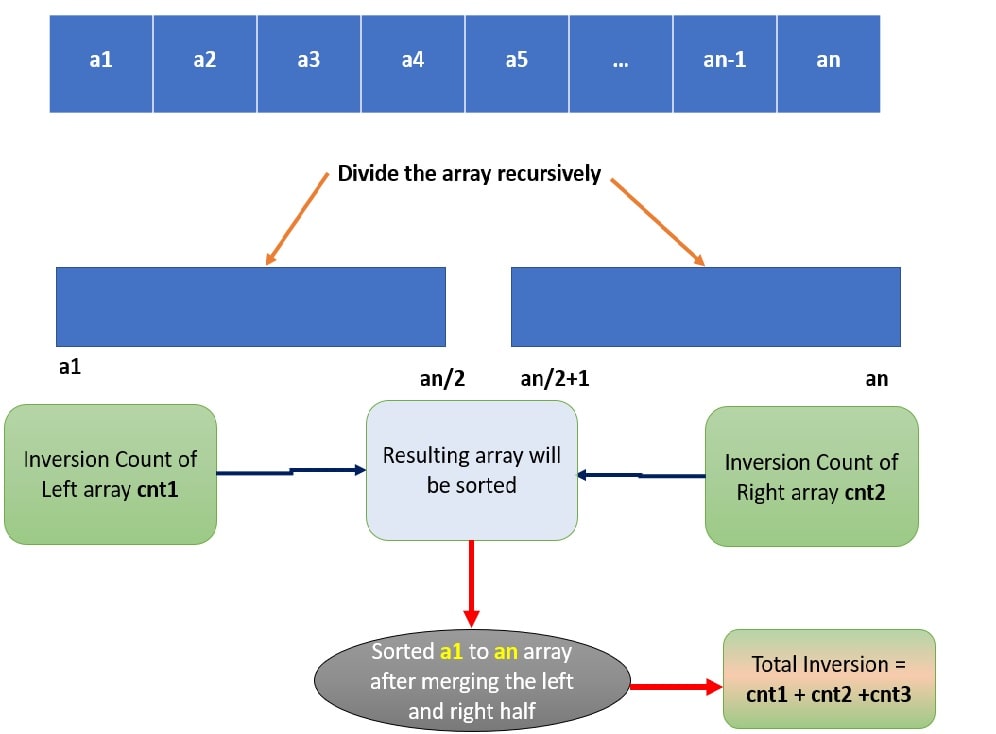
Steps to find the total inversion count using the Merge Sort:
You must know the recursion and Merge Sort algorithm to understand this example code. So it is my advice if you are not familiar with recursion and merge sort algorithm, you should read it. Now let’s see the steps to find the total inversion count of the given input array arr[left..right].
1. First, we need to divide the given input array into two halves recursively similar as in the case of merge sort. The recursion will continue until the base condition that is only one element is left.
2. In the recursive function we will count the number of inversions in the first half, the second half as well as the number of inversions during the merge process.
/*recursive function:left is for left index and
right is right index of the sub-array of arr to be sorted */
int mergeSort(int arr[], int temp[], int left, int right)
{
int mid;
int cnt1 =0, cnt2 = 0, cnt3 =0;
if (right > left)
{
//Middle point to divide the array into two halves
mid = (right + left) / 2;
//Inversion count of left and right parts
cnt1 += mergeSort(arr, temp, left, mid);
cnt2 += mergeSort(arr, temp, mid + 1, right);
//Inversion Counts during merging the tqo sorted parts
cnt3 += merge(arr, temp, left, mid + 1, right);
}
return (cnt1 + cnt2 + cnt3); //total inversion count;
}
3. Tricky part here to find the number of inversion count during the merge process. In which we will maintain the two variables 'i' and 'j', where'i' will point to the starting element of the left half and'j' will point to the starting element of the second half.
We will compare the elements at both positions. If the ith element is smaller than the jth element just add it to the new sorted list. Otherwise, increment the inversions count by (mid-i).
while ((i <= mid - 1) && (j <= right))
{
if (arr[i] <= arr[j])
{
temp[k++] = arr[i++];
}
else
{
temp[k++] = arr[j++];
//counting inversion see the above mentioned image
inv_count = inv_count + (mid - i);
}
}
Now let’s see the C code to find the inversion count using Merge Sort Algorithm for the given input array.
#include <stdio.h>
int merge(int arr[], int temp[], int left, int mid,
int right)
{
int i, j, k;
int inv_count = 0;
i = left; // i is index for left subarray
j = mid; // j is index for right subarray
k = left; // k is index for resultant merged subarray
while ((i <= mid - 1) && (j <= right))
{
if (arr[i] <= arr[j])
{
temp[k++] = arr[i++];
}
else
{
temp[k++] = arr[j++];
//counting inversion see the above mentioned image
inv_count = inv_count + (mid - i);
}
}
/* Copy the remaining elements of left subarray
(if there are any) to temp*/
while (i <= mid - 1)
{
temp[k++] = arr[i++];
}
/* Copy the remaining elements of right subarray
(if there are any) to temp*/
while (j <= right)
{
temp[k++] = arr[j++];
}
//Copy back the merged elements to original array
for (i = left; i <= right; i++)
{
arr[i] = temp[i];
}
return inv_count; // inversion count
}
/*recursive function:left is for left index and
right is right index of the sub-array of arr to be sorted */
int mergeSort(int arr[], int temp[], int left, int right)
{
int mid;
int cnt1 =0, cnt2 = 0, cnt3 =0;
if (right > left)
{
//Middle point to divide the array into two halves
mid = (right + left) / 2;
//Inversion count of left and right parts
cnt1 += mergeSort(arr, temp, left, mid);
cnt2 += mergeSort(arr, temp, mid + 1, right);
//Inversion Counts during merging the tqo sorted parts
cnt3 += merge(arr, temp, left, mid + 1, right);
}
return (cnt1 + cnt2 + cnt3); //total inversion count;
}
//The function returns the number of inversions in the array
int inversionCount(int arr[], int array_size)
{
int temp[array_size];
return mergeSort(arr, temp, 0, array_size-1);
}
int main()
{
int arr[] = { 3, 2, 1};
int arr_size = sizeof(arr) / sizeof(arr[0]);
int inversionCnt = inversionCount(arr, arr_size);
printf(" Number of inversions are %d \n",inversionCnt);
return 0;
}
Output:
Number of inversions are 3
Complexity Analysis of inversion count using Merge Sort:
Time Complexity: O(NlogN)
Space Complexity: O(N)
Recommended Articles for you:
- Best programming laptop for programmers.
- How do you reverse an array in C?
- C program to find the Median of two sorted arrays of different sizes.
- Basics of the recursive function.
- Merge Sort algorithm with example code.
- C program to rearrange array such that even positioned are greater than odd.
- How to rotate an array left and right by a given number K?
- Why is it faster to process sorted array than an unsorted array?
- How to access 2d array in C?
- How to remove duplicates from a given array in C?
- Array interview questions.
- How to create dynamic array in C?
- How to pass an array as a parameter in C?