counting sort algorithm

This blog post explains the counting Sort Algorithm and its implementation using the C programming language. So before writing the C code for the counting Sort let’s first understand the counting Sort.

 

What is counting Sort Algorithm:

Counting sort is not a comparison sort algorithm. The counting sort is an efficient sorting algorithm that can be used for sorting elements within a specific range. It sorts the elements of an array by counting the frequency (number of occurrences) of each unique element in the array.

The count/frequency of each unique element is stored in an auxiliary array and the sorting is done by mapping the count as an index of the auxiliary array.

Note: Counting sort is not a comparison sort algorithm and gives O(n) complexity for sorting. To achieve O(n) complexity, the counting sort assumes that each of the elements is an integer in the range 1 to N, for some integer N.

 

Counting Sort example code:

Now let’s see the example code for the Counting Sort using the C programming language.

#include <stdio.h>
#include<string.h>

void countingSort(int array[], int size)
{
    int output[size];
    int i = 0;

    // Find the largest element of the array
    int max = array[0];
    for (i = 1; i < size; i++)
    {
        if (array[i] > max)
        {
            max = array[i];
        }
    }

    // Create a count array to store count of individual
    // characters and initialize count array as 0
    int count[max+1];//C99 supports
    memset(count, 0, sizeof(count));


    // Store the count of each element
    for (i = 0; i < size; i++)
    {
        count[array[i]]++;
    }

    // Store the cummulative count of each array
    for (i = 1; i <= max; i++)
    {
        count[i] += count[i - 1];
    }

    // Find the index of each element of the original array in count array, and
    // place the elements in output array
    for (i = size - 1; i >= 0; i--)
    {
        output[count[array[i]] - 1] = array[i];
        count[array[i]]--;
    }

    // Copy the sorted elements into original array
    for (i = 0; i < size; i++)
    {
        array[i] = output[i];
    }
}


//print array element
void printArray(int arr[], int array_size)
{
    int i;
    for (i = 0; i < array_size; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}


int main()
{
    int arr[] = {18,4, 0, 2, 8, 9, 3, 1};

    //calculate array size
    int array_size  = sizeof(arr) / sizeof(arr[0]);

    countingSort(arr, array_size);

    printArray(arr, array_size);

    return 0;
}

Output:

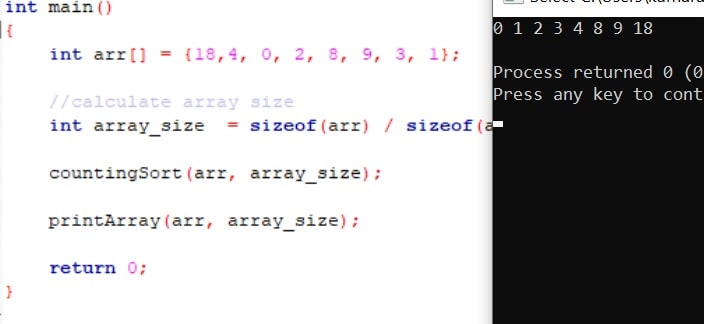
counting sort algorithm

 

Counting Sort Complexity:

Where k is the range of the non-negative key values.

Time Complexity
Best O(n+k)
Worst O(n+k)
Average O(n+k)
Space Complexity O(max)

 

Recommended Articles for you: