In this blog post, we learn how to write a C program to find the roots of a quadratic equation?. We will write the C program to find the roots of a quadratic equation using the if-else condition. Write C program to find roots of quadratic equation using switch statements. How to find all roots of a quadratic equation using if else in C programming. Logic to find roots of quadratic equation in C programming.

Let see an example,

Input  :  a = 1, b = -2, c = 1
Output:  Roots are real and same
          1

Input  :  a = 1, b = 7, c = 12
Output:  Roots are real and different
          -3, -4

Input  :  a = 1, b = 1, c = 1
Output :  Roots are complex 
          -0.5 + i1.73205
          -0.5 - i1.73205

Quadratic equation:

In algebra, a quadratic equation is an equation that can be rearranged in standard form as,

ax2 + bx + c = 0

Below is a direct formula for finding the roots of the quadratic equation.

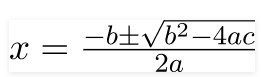
There are the following important cases of this formula.

Case 1: (Discriminant < 0)

b*b < 4*a*c, then roots are complex(not real).

For example roots of x2 + x + 1, roots are
-0.5 + i1.73205 and -0.5 - i1.73205

Case 2: (Discriminant == 0)

b*b == 4*a*c, then roots are real and both roots are the same.

For example, roots of x2 - 2x + 1 are 1 and 1

Case 3 (Discriminant > 0):

b*b > 4*a*c, then roots are real and different.

For example, roots of x2 - 7x - 12 are 3 and 4

C Program to Find the Roots of a Quadratic Equation using if-else:

The below program ask the user to enter the value of a,b and c. After getting the value from the user it will calculate on the basis of ‘Discriminant’ value.

#include <stdio.h>
#include <math.h>

int main()
{
    float a, b, c;
    float root1, root2, imaginary;
    float discriminant;

    printf("Enter value of a of quadratic equation (aX^2 + bX + c): ");
    scanf("%f", &a);

    printf("Enter value of b of quadratic equation (aX^2 + bX + c): ");
    scanf("%f",&b);


    printf("Enter values of c of quadratic equation (aX^2 + bX + c): ");
    scanf("%f",&c);

    // Find discriminant of the equation
    discriminant = (b * b) - (4 * a * c);


    //Check different cases for the discriminant
    if(discriminant > 0)
    {
        root1 = (-b + sqrt(discriminant)) / (2*a);
        root2 = (-b - sqrt(discriminant)) / (2*a);

        printf("Two distinct and real roots exists: %.2f and %.2f", root1, root2);
    }
    else if(discriminant == 0)
    {
        root1 = root2 = -b / (2 * a);

        printf("Two equal and real roots exists: %.2f and %.2f", root1, root2);
    }
    else if(discriminant < 0)
    {
        root1 = root2 = -b / (2 * a);
        imaginary = sqrt(-discriminant) / (2 * a);

        printf("Two distinct complex roots exists: %.2f + i%.2f and %.2f - i%.2f",
               root1, imaginary, root2, imaginary);
    }

    return 0;
}

Output:

Enter value of a of quadratic equation (aX^2 + bX + c): 2
Enter value of b of quadratic equation (aX^2 + bX + c): 7
Enter values of c of quadratic equation (aX^2 + bX + c): 2
Two distinct and real roots exist: -0.31 and -3.19

C program to find the roots of a quadratic equation using a function:

#include <stdio.h>
#include <math.h>


void printQuadraticRoots(float a, float b,float c)
{
    float root1, root2, imaginary;
    float discriminant;

    // Find discriminant of the equation
    discriminant = (b * b) - (4 * a * c);
    //Check different cases for the discriminant
    if(discriminant > 0)
    {
        root1 = (-b + sqrt(discriminant)) / (2*a);
        root2 = (-b - sqrt(discriminant)) / (2*a);
        printf("Two distinct and real roots exists: %.2f and %.2f", root1, root2);
    }
    else if(discriminant == 0)
    {
        root1 = root2 = -b / (2 * a);
        printf("Two equal and real roots exists: %.2f and %.2f", root1, root2);
    }
    else if(discriminant < 0)
    {
        root1 = root2 = -b / (2 * a);
        imaginary = sqrt(-discriminant) / (2 * a);
        printf("Two distinct complex roots exists: %.2f + i%.2f and %.2f - i%.2f",
               root1, imaginary, root2, imaginary);
    }

}

int main()
{
    float a, b, c;

    printf("Enter value of 'a' of quadratic equation (aX^2 + bX + c): ");
    scanf("%f", &a);

    printf("Enter value of 'b' of quadratic equation (aX^2 + bX + c): ");
    scanf("%f",&b);


    printf("Enter values of 'c' of quadratic equation (aX^2 + bX + c): ");
    scanf("%f",&c);


    printQuadraticRoots(a,b,c);

    return 0;
}

Output:

Enter value of ‘a’ of quadratic equation (aX^2 + bX + c): 5
Enter value of ‘b’ of quadratic equation (aX^2 + bX + c): 2
Enter values of ‘c’ of quadratic equation (aX^2 + bX + c): 2
Two distinct complex roots exists: -0.20 + i0.60 and -0.20 – i0.60