A prime number is a positive natural number, whose value greater than 1 and it has only two factors 1 and the number itself. Either you can say that prime numbers only divided by itself and 1. Any positive natural number who is not a prime number is called a composite number.
For example,
2,3,5,7,11..
In the above example, 2 is the (smallest) prime number because it has only two factors 1 and 2.
Note: 1 is not a prime or composite number and 2 is the only even prime number.
Using the trial division we can check the prime number in C but it is a slow method to check the prime number. In which we need to check whether given number n is a multiple of any integer between 2 and the square root of n.
We can also use faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always produces the correct answer in polynomial time but is too slow to be practical.
Algorithm to check prime number using trial division method
START
Step 1 → Take the number n
Step 2 → Divide the number n with (2, n-1) or (2, n/2) or (2, sqrt(n)).
Step 3 → if the number n is divisible by any number between (2, n-1) or (2, n/2) or (2, sqrt(n)) then it is not prime
Step 4 → If it is not divisible by any number between (2, n-1) or (2, n/2) or (2, sqrt(n)) then it is a prime number
STOP
Check Prime Number In C
Above I have discussed that there are many ways to find the prime number in C. In this blog post, I will discuss only the trial division method for another algorithm I have written separate articles. So let see some C programs to check prime numbers using the trial division method.
Example Code 1:
In the below code to check prime number, we are checking that the given number n is a multiple of any integer between 2 and (n -1) or not. If the given number n is a multiple of any integer between 2 and (n -1), then n will be not a prime number.
#include <stdio.h>
#define PRIME_NUMBER 1
int isPrimeNumber(int number)
{
int iLoop = 0;
int iPrimeFlag = 1;
//check for negative number and one
if(number <= 1)
{
iPrimeFlag = 0;
}
else
{
for(iLoop = 2; iLoop < number; iLoop++)
{
// check prime number
if((number % iLoop) == 0)
{
//update the flag when number is not prime
iPrimeFlag = 0;
break;
}
}
}
return iPrimeFlag;
}
int main()
{
int iRetValue = 0;
int number = 0;
printf("Enter the number : ");
scanf("%d",&number);
iRetValue = isPrimeNumber(number);
//Check for prime number
if (iRetValue == PRIME_NUMBER)
{
printf("\n\n%d is prime number..\n\n", number);
}
else
{
printf("\n\n%d is not a prime number..\n\n", number);
}
return 0;
}
Output:


Example 2:
In the below code to check prime number, we are checking that the given number n is a multiple of any integer between 2 and (n/2) or not. If the given number n is a multiple of any integer between 2 and (n/2), then n will be not a prime number.
This method is similar to example 1, In which we are just reducing the number of iteration to optimize the code.
#include <stdio.h>
#define PRIME_NUMBER 1
int isPrimeNumber(int number)
{
int iLoop = 0;
int iPrimeFlag = 1;
int iLimit = number/2; //Divide the number by 2
if(number <= 1)
{
iPrimeFlag = 0;
}
else
{
for(iLoop = 2; iLoop <= iLimit; iLoop++)
{
if((number % iLoop) == 0) // Check prime number
{
iPrimeFlag = 0;
break;
}
}
}
return iPrimeFlag;
}
int main()
{
int retvalue = 0;
int number = 0;
printf("Enter the number : ");
scanf("%d",&number);
retvalue = isPrimeNumber(number);
if (retvalue == PRIME_NUMBER)
{
printf("\n\n%d is prime number..\n\n", number);
}
else
{
printf("\n\n%d is not a prime number..\n\n", number);
}
return 0;
}
Output:


Example 3:
There is another efficient way to find the prime number. In the below code to check prime number, we are checking that the given number n is a multiple of any integer between 2 and the square root of n. or not. If the given number n is a multiple of any integer between 2 and the square root of n., then n will be not a prime number.
#include <stdio.h>
#include <math.h>
#define PRIME_NUMBER 1
int isPrimeNumber(int number)
{
int iLoop = 0;
int iPrimeFlag = 1;
int iLimit = sqrt(number); // calculate of square root n
if(number <= 1)
{
iPrimeFlag = 0;
}
else
{
for(iLoop = 2; iLoop <= iLimit; iLoop++)
{
if((number % iLoop) == 0) // Check prime number
{
iPrimeFlag = 0;
break;
}
}
}
return iPrimeFlag;
}
int main()
{
int retvalue = 0;
int number = 0;
printf("Enter the number : ");
scanf("%d",&number);
retvalue = isPrimeNumber(number);
if (retvalue == PRIME_NUMBER)
{
printf("\n\n%d is prime number..\n\n", number);
}
else
{
printf("\n\n%d is not a prime number..\n\n", number);
}
return 0;
}
Output:


Find all the prime numbers less than or equal to a given integer n by Eratosthenes’ method:
- First create a list of consecutive integers numbers from 2 to n: (2, 3, 4, …, n).
- Initially, let q equal 2, the smallest prime number.
- Find the all multiple of q by counting to n from 2q in increments of q, and mark them on the list. (these will be 2q, 3q, 4q, …; the q itself should not be marked).
- Find the first number greater than q in the list that is not marked. If there was no such number, stop. Otherwise, let q now equal this new number (which is the next prime), and repeat from step 3.
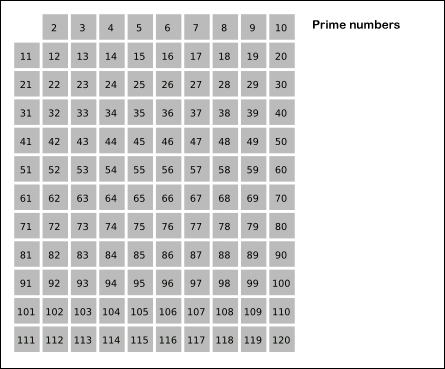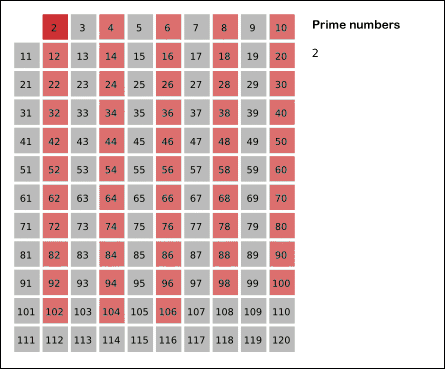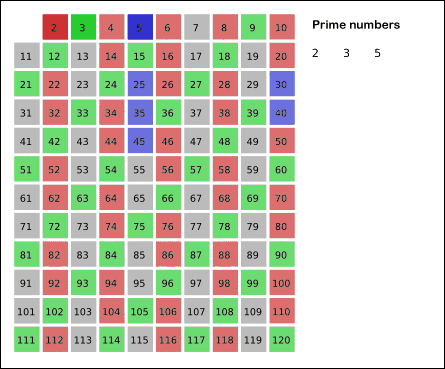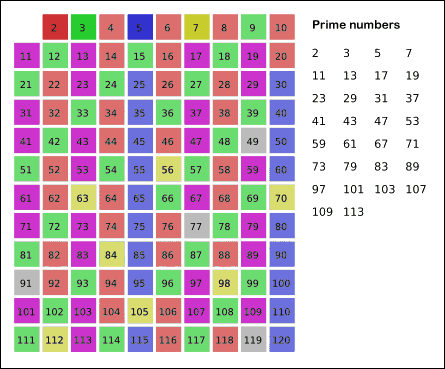
When the algorithm terminates, the numbers remaining not marked in the list are all the primes below n.
Algorithms of Sieve of Eratosthenes
Input: an integer n > 1
Let A be an array of Boolean values, indexed by integers 2 to n,
initially all set to true.
for i = 2, 3, 4, ..., not exceeding √n:
if A[i] is true:
for j = i2, i2+i, i2+2i, i2+3i, ..., not exceeding n :
A[j] := false
Output: all i for which A[i] is true is the prime number.
Steps to find all the prime numbers less than or equal to 15 using the above mentioned algorithm, proceed as follows.
- First, create an array of integers from 2 to 15 and initially mark all the elements as a prime number.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 - The first prime number in the list is 2, marked every number in the list, which is multiple of 2.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 - The next unmarked number in the list after 2 is 3, marked every number in the list, which is multiple of 3.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 - The next number not yet marked out in the list after 3 is 5, but 5*5 is greater than 15. So here we will stop the process because all members have been marked out at this point.
Note: All unmarked numbers on the list are prime numbers.
C program to find all prime number up to n
#include <stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>
void GetRangeOfPrimeNumber(const int n, char *pcRangePrimeNum)
{
int aIndex = 0;
//Set pcRangePrimeNum 1 from pcRangePrimeNum[0..n]
memset(pcRangePrimeNum, 1,(n+1));
pcRangePrimeNum[0] = 0;
pcRangePrimeNum[1] = 0;
int iLimit = sqrt(n);
for (aIndex=2; aIndex <= iLimit; aIndex++)
{
// If pcRangePrimeNum[aIndex] is not changed, then it is a prime
if (pcRangePrimeNum[aIndex] == 1)
{
int i;
// Update all multiples of p
for (i=aIndex*2; i<=n; i += aIndex)
{
pcRangePrimeNum[i] = 0;
}
}
}
}
// Driver Program to test above function
int main()
{
int n =0;
int iPrimeNumber =0;
char *pcPrimeNumber = NULL;
printf("Enter the number: ");
scanf("%d",&n);
if(n <= 1)
{
printf("\n\nIt is not a prime number\n\n");
return 0;
}
else
{
// Allocate memory for list
pcPrimeNumber = malloc(sizeof(char)*(n+1));
//Get the prime numbers
GetRangeOfPrimeNumber(n,pcPrimeNumber);
printf("\n\nThere are following prime numbers smaller than or equal to \n\n" );
// Print all the prime numbers
for (iPrimeNumber=2; iPrimeNumber<=n; iPrimeNumber++)
{
if (pcPrimeNumber[iPrimeNumber])
{
printf("prime %d\n",iPrimeNumber);
}
}
free(pcPrimeNumber); // free the allocated memory
}
return 0;
}
Output:
Recommended Articles for you:
- find all prime numbers up to n using trial division and Sieve of Eratosthenes algorithm.
- Check date validity in C?
- How to use if in C programming.
- How to use C if-else condition?
- Create an employee record system in C.
- Way to create a library management system in C.
- How to create student record system in C?
- How to use for loop in C?
- You should know while loop use.
- When we should use do while in the C program.
- Use of the switch case in the C program.
- C language character set.
- Elements of C Language.
- Data type in C language.
- Operators with Precedence and Associativity.
- How to pass an array as a parameter?
- Memory Layout in C.
- File handling in C, In a few hours.
- Replacing nested switches with the multi-dimensional array
- How to access a two-dimensional array using pointers?
- Brief Introduction of switch case in C.
- 100 C interview Questions.
- Function pointer in c, a detailed guide.
- How to use the structure of function pointer in c language?
- Function pointer in structure.
- Pointer Arithmetic in C.
- Brief Introduction of void pointer in C.
References:
https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
