
In the interview generally, bit reversal is the common question for the interviewer. There are several methods to reverse the bits of an integer.
If you have good knowledge of unary operators then bit reversal is a very simple question for you otherwise, it can be difficult.
So it is my personal advice before looking the example code read the unary operators and try this yourself first.
Note: Quiz on bit-wise operators.
Before going to example code I am discussing bit-wise operator which are frequently used in below example code.
There is some important list of the bitwise operator.
Operator |
Meaning |
| | (Bitwise OR) | Use to Set a Bit of a Register. |
| & (Bitwise AND) | Use to check a Bit of Register. |
| ^ (Bitwise EX-OR) | Use to toggle a Bit of a Register. |
| ~ ( Bitwise complement) | Use for the compliment. |
| << (Shift left) | Use to shift a sequence of Bit toward left. |
| >> (Shift right) | Use to shift a sequence of Bit toward Right |
Note: In the c language, printf lacks the ability to print the data in binary format. So here, I am creating a simple program to print the number in binary format.
Example code to print the data in binary format.
#define CHAR_BITS 8 // size of character
#define INT_BITS ( sizeof(int) * CHAR_BITS) //bits in integer
// Use to print the data in binary format
void PrintInBinary(unsigned n)
{
short int iPos;
for (iPos = (INT_BITS -1) ; iPos >= 0 ; iPos--)
{
(n & (1 << iPos))? printf("1"): printf("0");
}
}
In below section, I am describing 5 ways to reverse bits of an integer.
First Method:
This is a simple method, we take an integer tmp and putting set bits of the num in tmp until the num becomes zero. When num becomes zero then shift the remaining bits of temp through the count.
Let assume here is a number num (short int) which contains a value 0000000000001100. First, we assign the num value to the tmp and get the LSB of num.
After that, we iterate a loop until the num becomes zero with putting set bits in tmp. When num becomes zero then left shift tmp 12 times to get the exact reverse number 11000000000000.
#include <stdio.h>
#include <stdlib.h>
#define CHAR_BITS 8 // size of character
#define INT_BITS ( sizeof(int) * CHAR_BITS)
//function print in binary format
void PrintInBinary(unsigned n)
{
short int iPos;
for (iPos = (INT_BITS -1) ; iPos >= 0 ; iPos--)
{
(n & (1 << iPos))? printf("1"): printf("0");
}
}
//bit reversal function
unsigned int ReverseTheBits(unsigned int num)
{
unsigned int count = (INT_BITS -1);
unsigned int tmp = num; // Assign num to the tmp
num >>= 1; // shift num because LSB already assigned to tmp
while(num)
{
tmp <<= 1; //shift the tmp because alread have the LSB of num
tmp |= num & 1; // putting the set bits of num
num >>= 1;
count--;
}
tmp <<= count; //when num become zero shift tmp from the remaining counts
return tmp;
}
int main()
{
unsigned int data = 0;
unsigned int Ret = 0;
printf("Enter the number : ");
scanf("%u",&data);
printf("\n\nEntered Data is " );
PrintInBinary(data);
Ret = ReverseTheBits(data);
printf("\n\nReverse Data is " );
PrintInBinary(Ret);
return 0;
}
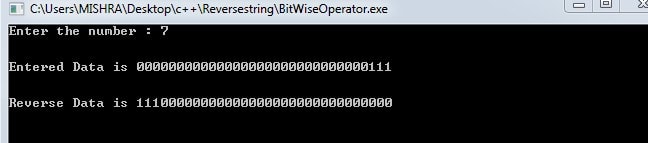
OutPut 1:
If you want to learn more about the c language, here 10 Free days (up to 200 minutes) C video course for you.
Second Method:
This method is similar to the first method. It is easy and less optimized as compared to the first method. In this method we take an integer tmp, putting set bits of num in tmp until the for loop runs. In every iteration of for loop we will shift the tmp in left direction ( tmp << 1 ) and num in the right direction (num >> 1).
#include <stdio.h>
#include <stdlib.h>
#define CHAR_BITS 8 // size of character
#define INT_BITS ( sizeof(int) * CHAR_BITS)
//print data in binary
void PrintInBinary(unsigned n)
{
short int iPos;
for (iPos = (INT_BITS -1) ; iPos >= 0 ; iPos--)
{
(n & (1 << iPos))? printf("1"): printf("0");
}
}
//bit reversal function
unsigned int ReverseTheBits(unsigned int num)
{
unsigned int iLoop = 0;
unsigned int tmp = 0; // Assign num to the tmp
int iNumberLopp = (INT_BITS - 1);
for(; iLoop < iNumberLopp; iLoop++)
{
tmp |= num & 1; // putting the set bits of num
num >>= 1; //shift the tmp Right side
tmp <<= 1; //shift the tmp left side
}
return tmp;
}
int main()
{
unsigned int data = 0;
unsigned int Ret = 0;
printf("Enter the number : ");
scanf("%u",&data);
printf("\n\nEntered Data is " );
PrintInBinary(data);
Ret = ReverseTheBits(data);
printf("\n\nReverse Data is " );
PrintInBinary(Ret);
return 0;
}
OutPut 2:
Third Method:
In this method, we will check the set bits of num and run the loop through all the bits of an integer. If we find the ith bits of num is set then just put 1 at the ((INT_BITS – 1) – ith ) position of tmp, where INT_BITS is the number of bits of an integer.
#include <stdio.h>
#include <stdlib.h>
#define CHAR_BITS 8 // size of character
#define INT_BITS ( sizeof(int) * CHAR_BITS)
//print data in binary
void PrintInBinary(unsigned n)
{
short int iPos;
for (iPos = (INT_BITS -1) ; iPos >= 0 ; iPos--)
{
(n & (1 << iPos))? printf("1"): printf("0");
}
}
//bit reversal function
unsigned int ReverseTheBits(unsigned int num)
{
unsigned int iLoop = 0;
unsigned int tmp = 0; // Assign num to the tmp
int iNumberLopp = (INT_BITS - 1);
for(; iLoop < iNumberLopp; iLoop++)
{
if((num & (1 << iLoop))) // check set bits of num
{
tmp |= 1 << ((INT_BITS - 1) - iLoop); //putting the set bits of num in tmp
}
}
return tmp;
}
int main()
{
unsigned int data = 0;
unsigned int Ret = 0;
printf("Enter the number : ");
scanf("%u",&data);
printf("\n\nEntered Data is " );
PrintInBinary(data);
Ret = ReverseTheBits(data);
printf("\n\nReverse Data is " );
PrintInBinary(Ret);
return 0;
}
OutPut 3:
Fourth Method:
It is a very simple algorithm to reverse the bits of the 32-bit integer. This algorithm uses the eight constant value for the reversing of the bits and takes five simple steps.
In below section, I am describing the functioning of each step.
Steps 1:
num = (((num & 0xaaaaaaaa) >> 1) | ((num & 0x55555555) << 1));
This expression use to swap the bits.
Let an example, suppose num is 0100, after the above expression it will be 1000.
Steps 2:
num = (((num & 0xcccccccc) >> 2) | ((num & 0x33333333) << 2));
Above expression uses to swap the 2 bits of a nibble. Suppose num is 10 00, after the above expression, it will be 00 01.
Steps 3:
num = (((num & 0xf0f0f0f0) >> 4) | ((num & 0x0f0f0f0f) << 4));
Expression use to swaps the nibbles. like if num is 0011 0010 then after the above expression it will be 0010 0011.
Steps 4:
num = (((num & 0xff00ff00) >> 8) | ((num & 0x00ff00ff) << 8));
This statement uses to swap the bytes of an integer. Let num is 00001000 00001100, after the above expression, it will be 00001100 00001000.
Steps 5:
((num >> 16) | (num << 16));
The above expression uses to swap the half-word of an integer. Means that if the num is 0000000011001110 1000100100000110, after the above result number will be 1000100100000110 0000000011001110.
#include <stdio.h>
#include <stdlib.h>
#define CHAR_BITS 8 // size of character
#define INT_BITS ( sizeof(int) * CHAR_BITS)
//print data in binary
void PrintInBinary(unsigned n)
{
short int iPos;
for (iPos = (INT_BITS -1) ; iPos >= 0 ; iPos--)
{
(n & (1 << iPos))? printf("1"): printf("0");
}
}
//bit reversal function
unsigned int ReverseTheBits(register unsigned int x)
{
x = (((x & 0xaaaaaaaa) >> 1) | ((x & 0x55555555) << 1));
x = (((x & 0xcccccccc) >> 2) | ((x & 0x33333333) << 2));
x = (((x & 0xf0f0f0f0) >> 4) | ((x & 0x0f0f0f0f) << 4));
x = (((x & 0xff00ff00) >> 8) | ((x & 0x00ff00ff) << 8));
return((x >> 16) | (x << 16));
}
int main()
{
unsigned int data = 0;
unsigned int Ret = 0;
printf("Enter the number : ");
scanf("%u",&data);
printf("\n\nEntered Data is " );
PrintInBinary(data);
Ret = ReverseTheBits(data);
printf("\n\nReverse Data is " );
PrintInBinary(Ret);
return 0;
}
OutPut 4:
Fifth Method:
This is the simplest method to reverse the bits of an integer. In which we create a table of the hex value from 0 to 255. In this method, we are performing the AND operation of data with 0xFF to calculate the index of the array.
In this algorithm, we need to calculate the index of the array (look-up table) four times to getting the appropriate value from the look-up table. After getting the corresponding value we perform the bit shifting operation to get the reverse value.
#include <stdio.h>
#include <stdlib.h>
#define CHAR_BITS 8 // size of character
#define INT_BITS ( sizeof(int) * CHAR_BITS)
//print data in binary
void PrintInBinary(unsigned n)
{
short int iPos;
for (iPos = (INT_BITS -1) ; iPos >= 0 ; iPos--)
{
(n & (1 << iPos))? printf("1"): printf("0");
}
}
//Fastest (lookup table):
static const unsigned char TableBitReverse[] =
{
0x00, 0x80, 0x40, 0xC0, 0x20, 0xA0, 0x60, 0xE0, 0x10, 0x90, 0x50, 0xD0, 0x30, 0xB0, 0x70, 0xF0,
0x08, 0x88, 0x48, 0xC8, 0x28, 0xA8, 0x68, 0xE8, 0x18, 0x98, 0x58, 0xD8, 0x38, 0xB8, 0x78, 0xF8,
0x04, 0x84, 0x44, 0xC4, 0x24, 0xA4, 0x64, 0xE4, 0x14, 0x94, 0x54, 0xD4, 0x34, 0xB4, 0x74, 0xF4,
0x0C, 0x8C, 0x4C, 0xCC, 0x2C, 0xAC, 0x6C, 0xEC, 0x1C, 0x9C, 0x5C, 0xDC, 0x3C, 0xBC, 0x7C, 0xFC,
0x02, 0x82, 0x42, 0xC2, 0x22, 0xA2, 0x62, 0xE2, 0x12, 0x92, 0x52, 0xD2, 0x32, 0xB2, 0x72, 0xF2,
0x0A, 0x8A, 0x4A, 0xCA, 0x2A, 0xAA, 0x6A, 0xEA, 0x1A, 0x9A, 0x5A, 0xDA, 0x3A, 0xBA, 0x7A, 0xFA,
0x06, 0x86, 0x46, 0xC6, 0x26, 0xA6, 0x66, 0xE6, 0x16, 0x96, 0x56, 0xD6, 0x36, 0xB6, 0x76, 0xF6,
0x0E, 0x8E, 0x4E, 0xCE, 0x2E, 0xAE, 0x6E, 0xEE, 0x1E, 0x9E, 0x5E, 0xDE, 0x3E, 0xBE, 0x7E, 0xFE,
0x01, 0x81, 0x41, 0xC1, 0x21, 0xA1, 0x61, 0xE1, 0x11, 0x91, 0x51, 0xD1, 0x31, 0xB1, 0x71, 0xF1,
0x09, 0x89, 0x49, 0xC9, 0x29, 0xA9, 0x69, 0xE9, 0x19, 0x99, 0x59, 0xD9, 0x39, 0xB9, 0x79, 0xF9,
0x05, 0x85, 0x45, 0xC5, 0x25, 0xA5, 0x65, 0xE5, 0x15, 0x95, 0x55, 0xD5, 0x35, 0xB5, 0x75, 0xF5,
0x0D, 0x8D, 0x4D, 0xCD, 0x2D, 0xAD, 0x6D, 0xED, 0x1D, 0x9D, 0x5D, 0xDD, 0x3D, 0xBD, 0x7D, 0xFD,
0x03, 0x83, 0x43, 0xC3, 0x23, 0xA3, 0x63, 0xE3, 0x13, 0x93, 0x53, 0xD3, 0x33, 0xB3, 0x73, 0xF3,
0x0B, 0x8B, 0x4B, 0xCB, 0x2B, 0xAB, 0x6B, 0xEB, 0x1B, 0x9B, 0x5B, 0xDB, 0x3B, 0xBB, 0x7B, 0xFB,
0x07, 0x87, 0x47, 0xC7, 0x27, 0xA7, 0x67, 0xE7, 0x17, 0x97, 0x57, 0xD7, 0x37, 0xB7, 0x77, 0xF7,
0x0F, 0x8F, 0x4F, 0xCF, 0x2F, 0xAF, 0x6F, 0xEF, 0x1F, 0x9F, 0x5F, 0xDF, 0x3F, 0xBF, 0x7F, 0xFF
};
int main()
{
unsigned int data = 0;
unsigned int Ret = 0;
printf("Enter the number : ");
scanf("%u",&data);
printf("\n\nEntered Data is " );
PrintInBinary(data);
//Getting reverse value
Ret = (TableBitReverse[data & 0xff] << 24) |
(TableBitReverse[(data >> 8) & 0xff] << 16) |
(TableBitReverse[(data >> 16) & 0xff] << 8) |
(TableBitReverse[(data >> 24) & 0xff]);
printf("\n\nReverse Data is " );
PrintInBinary(Ret);
return 0;
}
OutPut 5:
References: http://graphics.stanford.edu/~seander/bithacks.html#SwappingBitsXOR



thanks for the question